Στο κείμενο που ακολουθεί θα ασχοληθούμε με τη Θήρευση και θα εξετάσουμε διάφορα μαθηματικά μοντέλα που περιγράφουν συστήματα θηρευτή-θηράματος.΄Ετσι θα απαντήσουμε στο ερώτημα γιατί το ποσοστό των καρχαριών αυξήθηκε κατά τον Α΄Παγκόσμιο Πόλεμο και θα αναπτύξουμε τα συμπεράσματά μας.

Με βάση τα πληθυσμιακά δεδομένα που προκύπτουν για το σύστημα λαγού-λίγκας κατά την περίοδο 1845-1935 από τα βιβλία της εταιρίας που εμπορευόταν τα τομάρια των ζώων αυτών έχουμε ότι η μέγιστη πληθ. πυκνότητα του θηρευτή ακολουθεί τη μέγιστη πυκνότητα του θηράματος κάτι που εξηγείται ως εξής:΄Όταν ο πληθυσμός του θηράματος ελαττώνεται το θήραμα γίνεται όλο και πιο σπάνιο, επομένως φτάνει κάποτε η στιγμή που ο θηρευτής δυσκολεύεται να βρει το θήραμα.

Επίσης στη φάση αυτή οι θηρευτές είναι τόσο πολλοί που ανταγωνίζονται μεταξύ τους για την τροφή και άρα προκαλείται μείωση του θηρευτή.Ο πληθυσμός του θηράματος εξακολουθεί να μειώνεται για λίγο διάστημα αλλά όταν μειωθεί σε κάποιο χαμηλό σημείο ο πληθυσμός του θηράματος αρχίζει να ανακάμπτει.Ο πληθυσμός του θηρευτή εξακολουθεί να μειώνεται μέχρις ότου ο πληθυσμός του θηράματος έχει αυξηθεί αρκετά κι έτσι ο πληθυσμός του θηρευτή αρχίζει επίσης να αυξάνεται και πάλι.Αυτό συνεχίζεται μέχρις ότου οι θηρευτές αυξηθούν αρκετά και προκαλούν νέα πτώση του θηράματος.Ο κύκλος αρχίζει από την αρχή.

(2)

Ο πληθυσμός του θηράματος, εν απουσία του θηρευτή, αυξάνει εκθετικά (Νόμος αύξησης των πληθυσμών του Malthus) με ενδογενή ρυθμό αύξησης α. Αυτός ο ρυθμός αύξησης μειώνεται κατά bx όταν υπάρχουν θηρευτές.Δηλαδή ο αριθμός θανάτων του θηράματος είναι κατ΄ευθείαν ανάλογος του αριθμού των θηρευτών.Ο πληθυσμός του θηρευτή , εν απουσία του θηράματος, μειώνεται εκθετικά(Malthus) ενώ η πληθυσμιακή αύξηση του θηρευτή είναι κατ΄ ευθείαν ανάλογη του αριθμού του θηράματος.

Οι επιπτώσεις των αλληλεπιδράσεων μεταξύ των ατόμων είναι στιγμιαίες . Αυτό σημαίνει ότι δεν λαμβάνουμε υπ΄όψην την καθυστέρηση μεταξύ της στιγμής που ένας θηρευτής καταβροχθίζει ένα θήραμα και της στιγμής που η αφομοιωθείσα σάρκα μετουσιώνεται σε σώμα ενός νέου θηρευτή!!

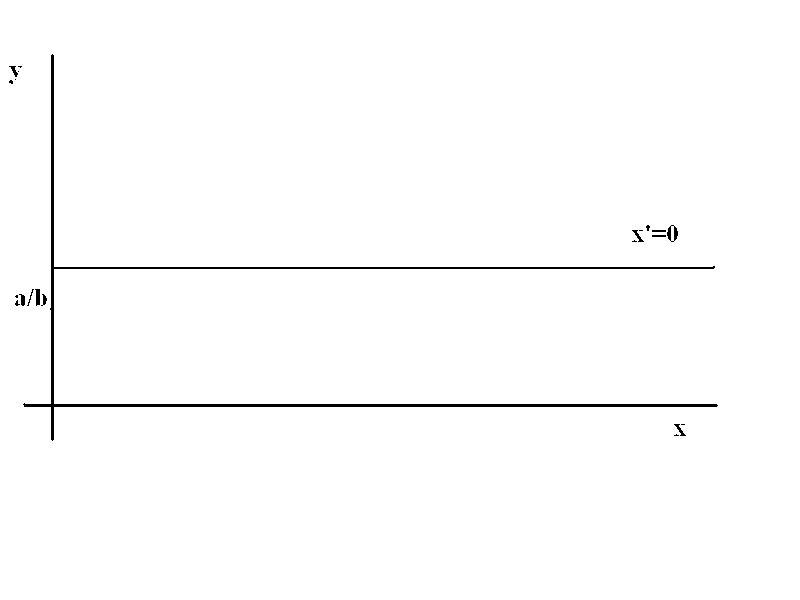
Για να διευκρινίσουμε την συμπεριφορά του συστήματος εργαζόμαστε ως εξής: Στο σύστημα συντεταγμένων x, y βρίσκουμε τον γεωμετρικό τόπο των σημείων που το θήραμα ισορροπεί( και τον γ. τ. των σημείων που το θήραμα αυξάνει και εκείνων που μειώνεται) . Από την (1) βλέπω ότι ο πληθυσμός του θηράματος ισορροπεί όταν

α-by=0

δηλ.σε όλα τα σημεία της ευθείας  y=α/b

Προφανώς το θήραμα αυξάνει σε όλα τα σημεία που α-by>0 δηλ. y<(α/b). ΄Ώστε για το θήραμα έχω:

Από την (2) βλέπω ότι ο πληθυσμός του θηρευτή ισορροπεί όταν -c+dx=0 δηλ. σε όλα τα σημεία της χ=c/d. ΄Ώστε για τον θηρευτή έχω:

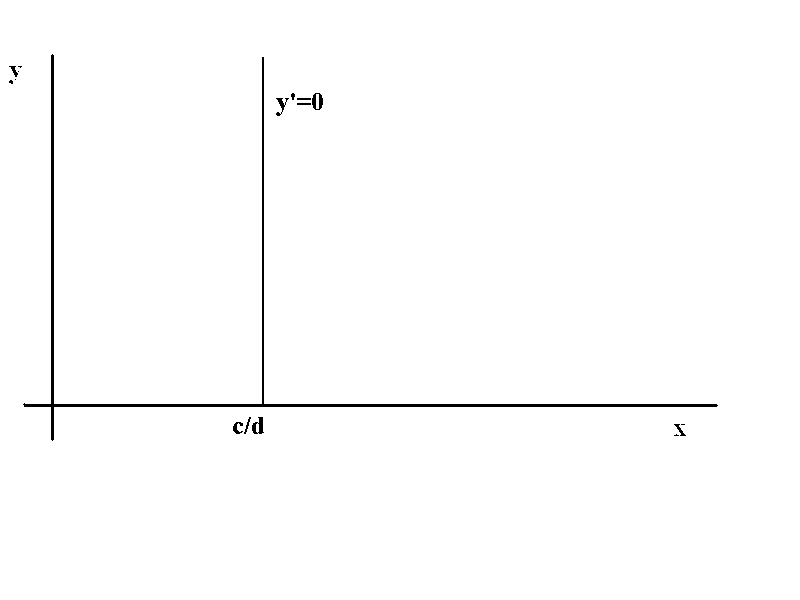
Τοποθετώντας τα δύο παραπάνω σχήματα σε ένα σύστημα καρτεσιανών συντεταγμένων έχω:

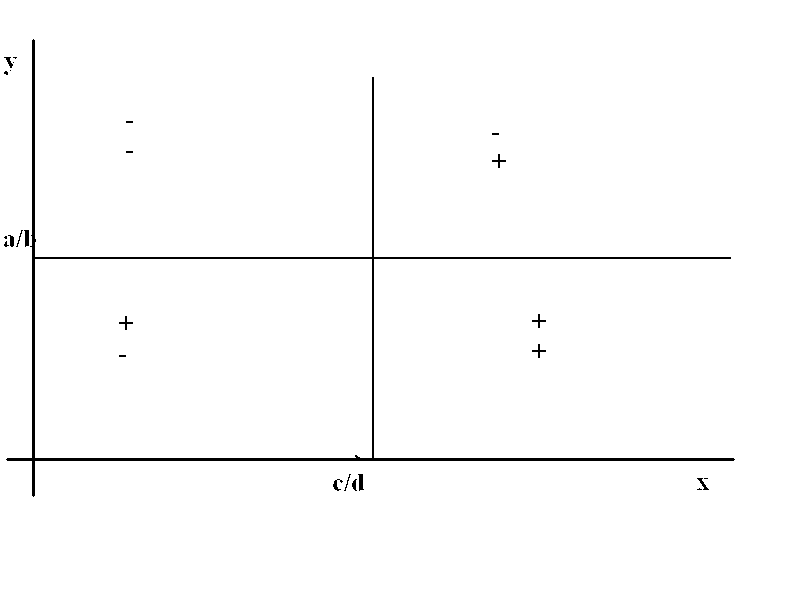
Το σημείο τομής των δύο ευθειών είναι το σημείο ουδέτερης ισορροπίας του συστήματος. Σε κάθε ζεύγος σημείων στο ανωτέρω σχήμα το επάνω αναφέρεται στην μεταβολή( αύξηση (+0) ή μείωση(-)) του πληθυσμού του θηράματος και το κάτω σημείο στην μεταβολή του θηρευτή.

Βλέπουμε ότι το σύστημα έχει αριστερόστροφες περιοδικές ταλαντώσεις.Το ύψος των ταλαντώσεων εξαρτάται από τους αρχικούς πληθυσμούς. Εάν το σύστημα άρχισε κοντά στο σημείο ισορροπίας του θα έχει ταλαντώσεις μικρού ύψους και εάν άρχισε μακριά από το σημείο ισορροπίας του θα έχει μεγάλες ταλαντώσεις. Συστήματα με αυτήν την συμπεριφορα ονομάζονται ‘συντηρητικά’ ή συστήματα ουδέτερης σταθερότητας.

**************

Το επόμενο βήμα μας θα είναι να λύσουμε το σύστημα των εξισώσεων (1) και (2).

Διαιρούμε κατά μέλη και οι λύσεις προκύπτουν αν λύσουμε την πρωτοτάξια δ. ε.

Αυτή η εξίσωση είναι διαχωρίσιμη αφού μπορεί να γραφεί στη μορφή:

κι επομένως ολοκληρώνουμε

για κάποια σταθερά k1

Παίρνοντας εκθετικά και στα δύο μέλη η παραπάνω σχέση δίνει:

(3)

για κάποια σταθερά Κ

Επομένως οι λύσεις του συστήματος είναι μια οικογένεια κλειστών καμπυλών στην οποία η κάθε καμπύλη της οικογένειας αντιστοιχεί σε μια διαφορετική τιμή της σταθεράς K.Η τιμή αυτή προσδιορίζεται από τις αρχικές τιμές των x και y.

**Στη συνέχεια θα δείξουμε ότι οι καμπύλες που ορίζει η εξίσωση (3) είναι κλειστές.**

Αρχικά θα προσδιορίσουμε την συμπεριφορά των συναρτήσεων

και για x,y>0. Επίσης θα πρέπει να σημειώσουμε   ότι f(0)=0,g(0)=0 και f(y)>0 για y>0.

Υπολογίζουμε κι έχουμε:

Βλέπουμε ότι η f έχει ένα απλό κρίσιμο στο y=a/b.Συνεπώς η f φτάνει τη μέγιστη τιμή της στο y=a/b ενώ η g-όμοια-φτάνει τη μέγιστη τιμή της στο x=c/d. Οι γραφικές παραστάσεις των f και g φαίνονται παρακάτω. Από τα παραπάνω προκύπτει ότι η εξίσωση (3) δεν έχει λύση x,y>0 για Κ>MxMy και έχει την απλή λύση x=c/d, y=a/b για Κ=ΜxMy.

Γι’αυτό πρέπει να μελετήσουμε μόνο την περίπτωση Κ=λΜ,όπου λ>0 και λ<Μy.Παρατηρούμε πρώτα ότι η εξίσωση λ= έχει μια λύση x=xm<c/d κι άλλη μία x=xμ>c/d.

Για το λόγο αυτό η εξίσωση

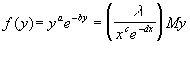
δεν έχει λύση y όταν το x είναι μικρότερο από το xm ή μεγαλύτερο από το xμ.΄Εχει μια απλή λύση y=a/b όταν x=xm ή x=xμ και δυο λύσεις y1(x) και y2(x) για κάθε x που ανήκει στο διάστημα (xm,xμ). Η μικρότερη λύση y1(x) είναι πάντοτε μικρότερη από a/b ενώ η μεγαλύτερη λύση y2(x) είναι πάντα πάνω από a/b.Καθώς το x τείνει είτε στο xm είτε στο xμ και οι δύο λύσεις y1,y2 πλησιάζουν το a/b. Συνεπώς οι καμπύλες οι οποίες καθορίζονται από την (3),είναι κλειστες.Επιπλέον καμία από τις καμπύλες αυτές (εκτός από το x=c/d, y=a/b) δεν περιέχει κάποιο από τα σημεία ισορροπίας του αρχικού συστήματος.΄Αρα όλες οι λύσεις του x(t),y(t) με x(0) και y(0) θετικά είναι περιοδικές συναρτήσεις του χρόνου.Αυτό μας λέει ότι κάθε λύση x(t),y(t) με x(0),y(0)>0 έχει την ιδιότητα x(t+T)=x(t) και y(t+T)=y(t) για κάποιο θετικό Τ. Ο Volterra χρησιμοποιώντας το ανωτέρω πρότυπο έκανε μια ενδιαφέρουσα παρατήρηση που την συμμερίζονται και πολλοί σύγχρονοι οικολόγοι.Παρατήρησε ότι εάν το θήραμα και ο θηρευτής μειωθούν κατά το ίδιο ποσοστό από έναν εξωτερικό παράγοντα στην συνέχεια ο πληθυσμός του θηράματος θα αυξηθεί γρηγορότερα από τον πληθυσμό του θηρευτή.

Η ερμηνεία βάση του προτύπου είναι ότι ποσοστιαία μείωση του γινομένου xy είναι μεγαλύτερη από τη μείωση του χ ή του y.Επειδή δε το xy στις εξισώσεις υπεισέρχεται αφενός μεν στο ρυθμό θανάτων του θηράματος αφ’ετέρου δε στον ρυθμό στον ρυθμό γεννήσεων του θηρευτή, συμπεραίνεται ότι η μείωση στον ρυθμό αυξήσεως του θηρευτή θα είναι μεγαλύτερη από την μείωση στον ρυθμό αυξήσεως του θηράματος.΄Ετσι ,τελικα, η πραγματική κατάσταση του συστήματος περιγράφεται από το σύστημα

Αυτό το σύστημα είναι ακριβώς το ίδιο με το πρώτο για α-κ>0,αν αντικαταστήσουμε το α-κ με α και το c+k με c.΄Ετσι η μέση τιμή των x(t) και y(t) θα είναι:

xμ=(c+k)/d ,yμ=(α-κ)/b

Έτσι,για παράδειγμα,ένα μετριασμένο και λογικό ποσό ψαρέματος(κ<α) στην πραγματικότητα αυξάνει τον αριθμό των ψαριών για διατροφή και μειώνει τα σαλάχια.Αντίθετα ένα μειωμένο επίπεδο αλιείας αυξάνει τα σαλάχια ενώ μειώνει τον πληθυσμό των ψαριών.Το αξιοθαύμαστο αυτό αποτέλεσμα ,γνωστό,ως αρχή του Volterra,εξηγεί τα αποτελέσματα του D’Anconna και λύνει εντελώς το πρόβλημά μας.Ας σημειώσουμε ακόμα ότι η παραπάνω αρχή έχει και μια άλλη ενδιαφέρουσα εφαρμογή:Οι εντομολόγοι έχουν παρατηρήσει ότι όταν προσπαθούν να καταπολεμήσουν κάποιο είδος φυτοφάγου εντόμου(θήραμα) με εντομοκτόνα,ο πληθυσμός του εντόμου συχνά επαναυξάνεται γρήγορα,σε επίπεδο μεγαλύτερο από το αρχικό.Το αποτέλεσμα αυτό αποδίδεται στην σύγχρονη μείωση των παρασίτων και θηρευτών του επιβλαβούς είδους.Σύμφωνα με την παρατήρηση του Volterra τα ωφέλιμα αυτά έντομα δεν μπορούν να επανέλθουν στα αρχικά τους επίπεδα τόσο γρήγορα,όσο τα επιβλαβή έντομα από τα οποία τρέφονται.